บทที่ 18 ความร้อน

บทที่ 18 ความร้อน

ความร้อน

ความร้อน (Thermal) ดูทฤษฎีความร้อนเพิ่มเติม(MS word )

                

ความร้อนเป็นพลังงานรูปหนึ่งที่เปลี่ยนมาจากพลังงานรูปอื่น เช่น พลังงานไฟฟ้า พลังงานกล (พลังงานศักย์และพลังงานจลน์) พลังงานเคมี พลังงานนิวเคลียร์ หรืองาน เป็นต้น

                พลังงานความร้อนมีหน่วยเป็นจูล (Joule, J ) ในระบบเอสไอ (SI) แต่บางครั้งอาจบอกเป็นหน่วยอื่นได้ เช่น แคลอรี (cal) และบีทียู (BTU)

                พลังงานความร้อน 1 แคลอรี คือพลังงานความร้อนที่ทำให้น้ำมวล  1  กรัม มีอุณหภูเพิ่มขึ้น  1 

 องศาเซลเซียส (^°C ) ในช่วง  14.5 ^°C ถึง  15.5 ^°C

               พลังงานความร้อน 1 บีทียู คือ พลังงานความร้อนที่ทำให้น้ำที่มีมวล  1  ปอนด์ มีอุณหภูมิเพิ่มขึ้น 1 

องศาฟาเรนไฮต์ (^°F) ในช่วง  58.1 ^°F ถึง  59.1 ^°F

                จากการทดลองพบว่า

                1  cal        =        4.186  J

                1  BTU      =        252  cal        =       1055  J

อุณหภูมิ

                นักวิทยาศาสตร์ได้กำหนดว่าอุณหภูมิ คือ ปริมาณที่แปรผันโดยตรงกับพลังงานจลน์เฉลี่ยของแก๊ส  การที่เราจะบอกว่าวัตถุใดร้อนมากหรือน้อย เราสามารถบอกได้ด้วยอุณหภูมิของวัตถุนั้น คือ วัตถุที่มีระดับความร้อนมากจะมีอุณหภูมิสูง วัตถุที่มีระดับความร้อนน้อยจะมีอุณหภูมิต่ำ  ดังนั้นถ้าเราเอาวัตถุที่มีอุณหภูมิสูงมาสัมผัสวัตถุที่มีอุณหภูมิต่ำ พลังงานความร้อนจะถูกถ่ายโอนจากวัตถุที่มีอุณหภูมิสูงไปยังวัตถุที่มีอุณหภูมิต่ำ จนวัตถุทั้งสองมีอุณหภูมิเท่ากัน

  อุปกรณ์ที่ใช้วัดอุณหภูมิเรียกว่า เทอร์โมมิเตอร์   เทอร์โมมิเตอร์มีหลายชนิด เช่น

1.  สเกลองศาเซลเซียส (Celsuis, ^°C) หรือบางที่เรียกว่าองศาเซนติเกรด (ที่ความดัน 1 บรรยากาศ จุดเยือกแข็งของน้ำเป็น 0  เซลเซียสและจุดเดือดเป็น 100  เซลเซียส ระหว่างจุดเยือกแข็งและจุดเดือดแบ่งเป็น 100 ส่วนเท่าๆ กัน )

2.  สเกลองศาเคลวิน (Kelvin, ^°K) เป็นหน่วยของอุณหภูมิสัมบูรณ์  (ที่ความดัน 1 บรรยากาศ จุดเยือกแข็งของน้ำเป็น  273.16  เคลวินและจุดเดือดเป็น  373.16  เคลวิน ระหว่างจุดเยือกแข็งและจุดเดือดแบ่งเป็น 100 ส่วนเท่าๆ กัน ) ##หน่วยเคลวินเป็นหน่วยมาตรฐานในระบบเอสไอ

ปริมาณความร้อนของวัตถุ (HEAT, Q)

เป็นพลังงานความร้อนที่วัตถุรับเข้ามาหรือคายออกไป จากการศึกษาผลของความร้อนต่อสสารหรือวัตถุในชั้นนี้จะศึกษาเพียงสองด้าน คือ

1. ความร้อนจำเพาะ ( Specific  heat )  หมายถึง พลังงานความร้อนที่ทำให้วัตถุมีอุณหภูมิสูงขึ้นหรือต่ำลงโดยสถานะยังคงรูปเดิม

2. ความร้อนแฝง (Latent  Heat) หมายถึง พลังงานความร้อนที่ทำให้วัตถุเปลี่ยนสถานะโดยอุณหภูมิคงที่

ความจุความร้อน ( Heat capacity, C ) คือความร้อนที่ทำให้สารทั้งหมดที่กำลังพิจารณามีอุณหภูมิเปลี่ยนไปหนึ่งหน่วย โดยสถานะไม่เปลี่ยน

ถ้าให้ปริมาณความร้อน ΔQ แก่วัตถุ ทำให้อุณหภูมิของวัตถุเปลี่ยนไป ΔT  ดังนั้นถ้าอุณหภูมิของวัตถุเปลี่ยนไป  1  หน่วย จะใช้ความร้อน  C คือ

   มีหน่วยเป็น จูล/เคลวิน (J/K)       

ความจุความร้อนจำเพาะ  (Specific  Heat capacity , c )  คือความร้อนที่ทำให้สาร(วัตถุ) มวลหนึ่งหน่วยมีอุณหภูมิเปลี่ยนไปหนึ่งองศาเคลวิน คือ 

   ความจุความร้อนจำเพาะของสาร(J/kg-K) 

นั่นคือ เมื่อสารมวล m มีอุณหภูมิเพิ่มจาก T₁ เป็น T₂ และความจุความร้อนจำเพาะมีค่าคงตัว ความร้อนที่สารได้รับ

คือ    

การเปลี่ยนสถานะของสาร

            สารและสิ่งของที่อยู่รอบตัวเราจะพบว่ามีอยู่  3  สถานะ คือ ของแข็ง (น้ำแข็ง) ของเหลว (น้ำ) และ

แก๊ส (ไอน้ำ) ได้

I.  ของแข็ง แรงดึงดูดระหว่างโมเลกุลมีค่ามาก ทำให้โมเลกุลอยู่ใกล้กัน จึงทำให้รูปทรงของของแข็งไม่เปลี่ยนแปลงมากเมื่อมีแรงขนาดไม่มากนักมากระทำ ตามคำจำกัดความนี้ เหล็ก คอนกรีต ก้อนหิน เป็นของแข็ง

II.  ของเหลว แรงดึงดูดระหว่างโมเลกุลมีค่าน้อย โมเลกุลจึงเคลื่อนที่ไปมาได้บ้าง จึงทำให้รูปทรงของของเหลวเปลี่ยนแปลงไปตามภาชนะที่ที่บรรจุ น้ำ น้ำมัน ปรอท เป็นของเหลว

III.  แก๊ส  แรงดึงดูดระหว่างโมเลกุลมีค่าน้อยมาก จนโมเลกุลของแก๊สอยู่ห่างกันมากและเคลื่อนที่ได้สะเปะสะปะ ฟุ้งกระจายเต็มภาชนะที่บรรจุ เช่นอากาศและแก๊สชนิดต่างๆ

 สถานการณ์จำลอง แสดงให้เห็นการเปลี่ยนแปลงของสสาร( น้ำ ) เมื่อได้รับความร้อน

    

การขยายตัวของวัตถุเนื่องจากความร้อน

            วัตถุโดยทั่วไปเมื่อได้รับความร้อนจะขยายตัว การขยายตัวของวัตถุจะขึ้นอยู่กับรูปร่างคือ

• วัตถุที่มีความยาวมีลักษณะเป็นเส้นหรือแท่งยาว จะมีการขยายตัวตามเส้น (การขยายตัวตามยาว)
• วัตถุที่เป็นแผ่นจะมีการขยายตัวตามพื้นที่
• วัตถุที่มีรูปร่างเป็นปริมาตรจะมีการขยายตัวตามปริมาตร

 ในทางกลับกันถ้าวัตถุสูญเสียความร้อนก็จะหดตัว

   

สมบัติที่สำคัญๆ เกี่ยวกับการขยายของของแข็ง ได้แก่

            1.  ของแข็งต่างชนิดกัน ถ้าเดิมมีความยาวเท่ากัน เมื่อร้อนขึ้นเท่ากันจะมีส่วนขยายตัวเพิ่มขึ้นไม่เท่ากัน

            2.  ของแข็งชนิดเดียวกัน ถ้าเดิมมีความยาวเท่ากัน เมื่อร้อนขึ้นเท่ากันจะมีส่วนขยายตัวเพิ่มขึ้นเท่ากัน

            3.  การขยายตัวของวัตถุเป็นเรื่องที่สำคัญมากในทางวิศวกรรม เช่น การวางเหล็กรางรถไฟ การขึงสายไฟฟ้าแรงสูงเป็นต้น

การถ่ายโอนความร้อน (Heat Transfer)

ความร้อนจะถ่ายโอนหรือส่งผ่านจากวัตถุที่ระดับความร้อนสูง (อุณหภูมิสูง) ไปสู่วัตถุที่มีระดับความร้อนต่ำ (อุณหภูมิต่ำ) การถ่ายโอนความร้อนมี  3  แบบ คือ

รูป แสดงการถ่ายโอนความร้อนแบบต่าง ๆ 

        1. การนำ เป็นการถ่ายโอนพลังงานความร้อนผ่านตัวกลางซึ่งโดยมากจะเป็นพวกโลหะต่างๆ เช่น เราเอามือไปจับช้อนโลหะที่ปลายข้างหนึ่งแช่อยู่ในน้ำร้อน มือเราจะรู้สึกร้อน เพราะความร้อนถูกส่งผ่านจากน้ำร้อนมายังมือเราโดยมีช้อนโลหะเป็นตัวนำความร้อน

        2. การพา  เป็นการถ่ายโอนความร้อนโดยการเคลื่อนที่ของโมเลกุลของตัวกลางเป็นตัวพาความร้อนไปจากบริเวณที่ระดับความร้อนสูง (อุณหภูมิสูง) ไปสู่บริเวณที่มีระดับความร้อนต่ำ (อุณหภูมิต่ำ) เช่นเวลาต้มน้ำ ความร้อนจากเตาทำให้น้ำที่ก้นภาชนะร้อนจะขยายตัวทำให้มีความหนาแน่นน้อยกว่าน้ำด้านบนจึงลอยตัวสูงขึ้นส่วนน้ำด้านบนที่มีอุณหภูมิต่ำกว่าและความหนาแน่นมากก็จะจมลงมาแทนที่ การหมุนวนของน้ำทำให้เกิดการพาความร้อน

        3. การแผ่รังสี  เป็นการส่งพลังงานความร้อนที่อยู่ในรูปคลื่นแม่เหล็กไฟฟ้า (รังสีอินฟราเรด) ดังนั้นจึงไม่ต้องอาศัยตัวกลางในการเคลื่อนที่ เช่นการแผ่รังสีความร้อนจากดวงอาทิตย์มายังโลก โดยทั่วไปวัตถุที่แผ่รังสีได้ดีก็จะรับ(ดูดกลืน)รังสีได้ดีด้วย วัตถุชนิดนั้นเราเรียกว่าวัตถุดำ (Black Body) วัตถุดำไม่มีในธรรมชาติ มีแต่ในอุดมคติ ดังนั้นวัตถุที่มีลักษณะใกล้เคียงวัตถุดำคือ วัตถุที่มีสีดำ ในทางกลับกันวัตถุขาวจะไม่ดูดกลืนรังสีและ  ไม่แผ่รังสีที่ตกกระทบ มีแต่ในอุดมคติเท่านั้น

  

สมดุลความร้อน

 ปริมาณความร้อนที่วัตถุอุณหภูมิสูงคายออกมาหรือลดลง จะเท่ากับปริมาณความร้อนที่วัตถุอุณหภูมิต่ำได้รับเข้าไปหรือเพิ่มขึ้น ซึ่งอาจกล่าวสั้นๆ ว่า"ความร้อนลดเท่ากับความร้อนเพิ่ม"

อออออ หรือเขียนเป็นความสัมพันธ์ได้ว่า

ออออออออออออออออออออออvvvvvvvvอออออออออ ΔQ_ลด = ΔQ_{เพิ่ม}

ขั้นตอนการแก้ปัญหาโจทย์เรื่องสมดุลความร้อน มีขั้นตอนดังนี้

1. แยกวัตถุออกเป็น 2 พวก คือ พวกอุณหภูมิสูงและพวกอุณหภูมิต่ำ แล้วเขียนแผนภาพ

2. หาปริมาณความร้อนที่วัตถุอุณหภูมิสูงลดลงหรือคายออกมาทั้งหมด หรืออาจเปลี่ยนสถานะ จาก ΔQ = mcΔT  หรือ   ΔQ = mL

3. หาปริมาณความร้อนที่วัตถุอุณหภูมิต่ำเพิ่มขึ้นหรือได้รับมาทั้งหมด หรืออาจเปลี่ยนสถานะ จาก ΔQ = mcΔT  หรือ   ΔQ = mL

4. ตั้งสมการ ΔQ_ลด = ΔQ_{เพิ่ม} แล้วแทนค่า ΔQ ที่ได้จากข้อ 2 และข้อ 3 ลงในแต่ละข้างของสมการ

การประยุกต์ใช้

อออออ ความรู้เรื่องสมดุลความร้อนนั้นมีการนำมาประยุกต์ใช้งานอย่างแพร่หลาย ตัวอย่างหนึ่งที่เห็นได้ชัดเจน คือ ระบบระบายความร้อนไม่ว่าจะเป็นในรถยนต์ เครื่องปรับอากาศ หรือในระบบหนึ่งๆของโรงงานอุตสาหกรรม เรามักจะสังเกตได้ว่าโรงงานอุตสาหกรรมมักจะอยู่ใกล้แหล่งน้ำหรือมีบ่อพักน้ำขนาดใหญ่เพื่อกักเก็บน้ำไว้ใช้สำหรับระบบหล่อเย็นเครื่องจักรกลบางประเภท ท่านจะได้ศึกษาการคำนวณเกี่ยวกับระบบระบายความร้อนจากตัวอย่างต่อไปนี้

ตัวอย่าง โรงไฟฟ้าต้องการระบายความร้อนทิ้งในอัตรา 4000 kJ/s โดยใช้น้ำจากสระเป็นตัวรับความร้อนผ่านอุปกรณ์แลกเปลี่ยนความร้อน ซึ่งมีประสิทธิภาพในการแลกเปลี่ยนความร้อน 80%  จงหาว่าน้ำในสระมีอุณหภูมิเริ่มต้น 20 °C และสระมีปริมาตร 1000 ลูกบาศก์เมตร ภายในเวลา 1 ชั่วโมง น้ำในสระจะมีอุณหภูมิเพิ่มขึ้นกีองศาเซลเซียส (ค่าความจุความร้อนจำเพาะของน้ำ 4 kj/kg.K และประสิทธิภาพในการแลกเปลี่ยนความร้อน คือ อัตราส่วนระหว่างปริมาณความร้อนที่ถ่ายเทจริงต่อปริมาณความร้อนสูงสุด)

วิธีทำ จากโจทย์วัตถุที่คายความร้อนออกมาคือโรงงานไฟฟ้า ส่วนวัตถุที่รับความร้อนเข้าไปคือน้ำในสระ โดยประสิทธิภาพในการแลกเปลี่ยนความร้อน 80% หมาบความว่า

ออออออออออออออออออออออออออออออออออ (80/100 )ΔQ_ลด = ΔQ_{เพิ่ม}

หรือ  ΔQ_น้ำ = (80/100)ΔQ_{ระบาย}

 mcΔT = 0.8 P.t

ρVΔT = 0.8 P.t      (m=ρV และ P คือ พลังงานความร้อนที่ระบายออกต่อหน่วยเวลาหรืออัตราการระบายความร้อน)

1000 x 1000 x 4000 x ΔT = 0.8 x 4000 x 1000 x 3600

ΔT =2.9 °C

    

      
  จากการทดลองและข้อสรุปของนักวิทยาศาสตร์หลายๆ คนที่ศึกษาเรื่องแก๊สเราจะเห็นว่า สมบัติของแก๊สมีความสัมพันธ์กันด้วยตัวแปรคล้ายๆ กัน คือ ทุกคนต่างก็ดูที่ปริมาตรของแก๊สที่เปลี่ยนไป ด้วยการกำหนดตัวแปรต้นแตกต่างกันออกไป
        บอยล์ เมื่อเปลี่ยนความดันของแก๊ส ปริมาตรจะเป็นอย่างไร
        ชาร์ล เมื่อเปลี่ยนอุณหภูมิของแก๊ส ปริมาตรจะเป็นอย่างไร
        อาโวกาโดร เมื่อเปลี่ยนจำนวนโมลหรือจำนวนโมเลกุลของแก๊ส ปริมาตรจะเป็นอย่างไร
        และทุกคนก็ได้ข้อสรุปดังที่ได้นำเสนอกฏของทุกคนมาแล้ว ถ้าเรารวบรวมกฎที่เกี่ยวกับแก๊สที่กล่าวมาแล้วทั้งหมด เราจะได้ความสัมพันธ์ดังนี้

จาก

กฏของบอยล์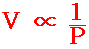        

กฎของชาร์ล          

กฏของอาโวกาโดร    

        เราสามารถรวมกฎทั้งสามนี้เข้าเป็นสมการรวมเพียงสมการเดียวได้ดังนี้

เมื่อ

P = ความดัน

V = ปริมาตร

n = จำนวนโมล

T = อุณหภูมิ(เคลวิน,K)

สมการนี้เรียกว่า สมการแก๊สในอุดมคติ

        R     =      ค่าคงที่ของแก๊ส  (gas constant)

        จากตัวแปรทั้ง 4 ตัว คือ ความดัน(P), ปริมาตร(V), จำนวนโมล(n) และอุณหภูมิ(T) เราสามารถหาค่า R ได้จากการแทนค่าตัวแปรทั้งสี่ในสมการแก๊สอุดมคติ

        แก๊สอุดมคติ 1 โมล ที่สภาวะมาตรฐาน ความดันเท่ากับ 1 บรรยากาศ อุณหภูมิ 273 K มีปริมาตร 22.4 ลิตร เราจะสามารถคำนวณหาค่าคงที่ของแก๊สได้ดังนี้

จาก    

นอกจากนี้ค่าคงที่ R ยังมีได้อีกในหลายหน่วย ดังนี้

        แก๊สใดๆ ก็ตามที่มีพฤติกรรมเป็นไปตามกฏนี้ จะเรียกแก๊สนั้นว่าแก๊สที่มีพฤติกรรมในอุดมคติ หรือแก๊สอุดมคติ หรือแก๊สสมบูรณ์แบบ (ideal gas)

ตัวอย่างการใช้กฎของแก๊สอุดมคติ ในการคำนวณ

ตัวอย่าง 1   น้ำจำนวน 1 กรัม ระเหยกลายเป็นไอในภาชนะขนาด 10 ลิตร ความดันของน้ำจะเป็นเท่าใดเมื่อการระเหยเป็นไอสมบูรณ์ที่อุณหภูมิ  200 องศาเซลเซียส

วิธีคำนวณ

จาก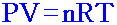     

เราต้องการหาความดันของไอน้ำ

จำนวนโมล (n) ของน้ำ

และอุณหภูมิสัมบูรณ์ เท่ากับ

แทนค่า V = 10 L , T = 473 K และ  n = 0.056 mol

ความดันจะเท่ากับ

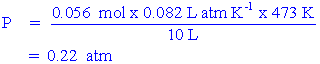
ตัวอย่าง 2    บอลลูนลูกหนึ่งบรรจุแก๊สฮีเลียม (He) หนัก 30 กิโลกรัม บอลลูนลูกนี้จะมีปริมาตรเท่าใด ถ้าความดันของแก๊สฮีเลียมเป็น 1.15 atm ณ อุณหภูมิ 20 องศาเซลเซียส

วิธีทำ

                  จาก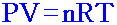         

                  เราอยากทราบปริมาตรของบอลลูน

                  ก่อนอื่นต้องคำนวณหา จำนวนโมลของแก๊สฮีเลียม หนัก 30 กิโลกรัม ก่อน

                  เราทราบมาแล้วว่า    ฮีเลียมจำนวน 1 โมล มีน้ำหนัก 4 กรัม หรือ      0.0040 kg

                                                                

                                                      อุณหภูมิต้องเปลี่ยนเป็นหน่วยเคลวินก่อน

ดังนั้น ปริมาตรสามารถคำนวณได้ดังนี้

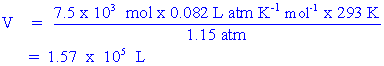
กฎของบอยล์ (Boyle's Law)

เมื่อทดลองโดยใช้การกดและดึงก้านกระบอกฉีดยา สามารถใช้ทฤษฎีจลน์ของแก๊สอธิบายได้ว่าเมื่อปริมาตรของแก๊สในกระบอกฉีดยาลดลง

ทำให้โมเลกุลของแก๊สอยู่ใกล้กันมากขึ้น จึงเกิดการชนกันเองและชนผนังภาชนะมากขึ้น เป็นผลให้ความดันของแก๊สในกระบอกฉีดยาเพิ่มขึ้นเมื่อเทียบกับตอนเริ่มต้น ในทางตรงกันข้ามการเพิ่มปริมาตรของแก๊สในกระบอกฉีดยาทำให้โมเลกุลของแก๊สอยู่ห่างกัน การชนกันเองของโมเลกุลของแก๊สและการชนผนังภาชนะน้อยลง ความดันของแก๊สในกระบอกฉีดยาจึงลดลง

จากผลการทดลองพบว่า ผลคูณของความดันกับปริมาตร (PV) ของแก๊สในการทดลองแต่ละครั้งมีค่าค่อนข้างคงที่ และพบว่าขณะที่อุณหภูมิคงที่

ถ้าปริมาตรของแก๊สเพิ่มขึ้นจะทำให้ความดันของแก๊สลดลง และเมื่อปริมาตรของแก๊สลดลง ความดันของแก๊สจะเพิ่มขึ้น

กฎของเกย์ ลูสแซก

เกย์–ลูสแซกได้ทำการทดลอง โดยให้ปริมาตรของแก๊สคงที่ เพื่อที่จะหาความสัมพันธ์ระหว่างความดันกับอุณหภูมิ ผลที่ได้คือ ความดันของ

แก๊สใด ๆ จะแปรผันตรงกับอุณหภูมิเมื่อปริมาตรคงที่

ดังนั้น

กฎรวมแก๊ส ได้จากการนำเอากฎของบอยล์  กฎของชาร์ล  มารวมกันจะได้  ความสัมพันธ์ของ  P,  V,  T    ดังนี้
กฎของบอยล์  V   ∞    1             เมื่ออุณหภูมิและมวลของแก๊สคงที่
                               P
กฎของชาร์ล  V    ∞    T                เมื่อความดันและมวลของแก๊สคงที่
 ดังนั้น          V    ∞    T
                                P 
                  V     =    kT
                                P       
             PV       =      k 
              T 
  หรือ     P₁V₁     =     P₂V₂
              T₁               T₂           
ตัวอย่างที่ 1  แก๊สชนิดหนึ่งปริมาตร  3  dm³  บรรจุในภาชนะภายใต้ความดัน  740  mmHg
อุณหภูมิ  80 ํC  ปริมาตรของแก๊สนี้ที่  STP  จะเท่ากับกี่ลูกบาศก์เดซิเมตร

วิธีทำ  จากสูตร           P₁V₁     =     P₂V₂
                                T₁               T₂                     
    740 mmHg X 3 dm³           =     760 mmHg X V₂
           273 + 80 K                               273 K
     740 mmHg X 3 dm³          =      760 mmHg X V₂
             353 K                                      273 K
                      V₂                  =      740 mmHg X 3 dm³ X 273 K
                                                        353 K X 760 mmHg
    
                      V₂                  =           2.26     dm³

ตัวอย่างที่  2  แก๊สแอมโมเนียจำนวนหนึ่งวัดปริมาตรได้  10   ลิตร ที่  15 ํC และ  720  ทอรร์
 จงหาปริมาตรของแก๊สนี้ถ้าเพิ่มอุณหภูมิเป็น  27 ํC  และความดันเป็น  780  ทอรร์

วิธีทำ  จากสูตร        P₁V₁     =       P₂V₂
                              T₁                 T₂          
       720 torr X  10 L          =      780 torr X  V₂
           273 + 15 K                     273 + 27  K

         720 torr X  10 L        =      780 torr X  V₂
               288 K                             300  K
                V₂                    =      720 torr X 10 L X 300 K
                                                      288 K X 780 torr      
                                        =           9.62     L
            ปริมาตรของแก๊สนี้    =           9.62     ลิตร  

   ทฤษฎีจลน์ของแก๊ส

เป็นทฤษฎีที่ตั้งขึ้นเพื่อใช้อธิบายกฎ ปรากฏการณ์ หรือผลการทดลองที่เกี่ยวกับแก๊ส และพฤติกรรมของแก๊ส

1. แก๊สประกอบด้วยอนุภาคจำนวนมากที่มีขนาดเล็กมาก จนถือได้ว่าอนุภาคของแก๊สไม่มีปริมาตรเมื่อเทียบกับขนาดภาชนะที่บรรจุ

2. โมเลกุลของแก๊สอยู่ห่างกันมาก ทำให้แรงดึงดูดและแรงผลักระหว่างโมเลกุลน้อยมาก จนถือได้ว่าไม่มีแรงกระทำต่อกัน

3. โมเลกุลของแก๊สเคลื่อนที่อย่างรวดเร็วในแนวเส้นตรง เป็นอิสระ ด้วยอัตราเร็วคงที่ และไม่เป็นระเบียบ จนกระทั่งชนกับโมเลกุลอื่น ๆ หรือชนกับผนังภาชนะจึงจะเปลี่ยนทิศทางและอัตราเร็ว

4. โมเลกุลของแก๊สที่ชนกันเองหรือชนกับผนังภาชนะจะเกิดการถ่ายโอนพลังงานให้แก่กันได้ แต่พลังงานรวมของระบบคงที่

5. ณ อุณหภูมิเดียวกัน โมเลกุลของแก๊สแต่ละโมเลกุลเคลื่อนที่ด้วยอัตราเร็วไม่เท่ากัน แต่จะมีพลังงานจลน์เฉลี่ยเท่ากัน โดยที่พลังงานจลน์เฉลี่ยของแก๊สจะแปรผันตรงกับอุณหภูมิเคลวิน

+ แก๊สที่มีสมบัติเป็นไปตามทฤษฎีจลน์ของแก๊สทุกประการเรียกว่า แก๊สอุดมคติ (Ideal gas) โดยปกติแก๊สทั่วไปจะมีสมบัติเคียงกับแก๊สอุดมคติเท่านั้น สำหรับแก๊สที่มีอนุภาคขนาดเล็ก เมื่อควบคุมให้อยู่ในภาวะที่มีปริมาตรมาก ความดันต่ำ และอุณหภูมิสูง จะมีสมบัติใกล้เคียงกับแก๊สอุดมคติมากขึ้น โดยเฉพาะแก๊สเฉื่อยจะมีสมบัติใกล้เคียงกับแก๊สอุดมคติมากจนอาจจัดเป็นแก๊สอุดมคติได้

      

  พลังงานภายในของระบบ (ใช้สัญลักษณ์เป็น E หรือ U) คือ ผลรวมของพลังงานอันเนื่องมาจาก
                            พลังงานจากการเคลื่อนที่, การสั่น และการหมุนของโมเลกุล
                            พลังงานจากการเคลื่อนที่ของอิเล็กตรอน โปรตอน และนิวตรอน
                            พลังงานอันเนื่องมาจากแรงกระทำระหว่างอนุภาคต่าง ๆ ในโมเลกุล
                            พลังงานจากตัวสสารเอง เช่น พลังงานนิวเคลียร์
                            พลังงานรูปอื่นๆ
การเปลี่ยนแปลงพลังงานภายใน มีค่าเท่ากับ งานรวมกับความร้อน

DE    =     w    +    q

จากที่เราทราบกันว่า ทั้งงานและความร้อนไม่ใช่ฟังก์ชันสภาวะ แล้วนักเรียนคิดว่า การเปลี่ยนแปลงพลังงานภายใน (DE) จะเป็นฟังก์ชันสภาวะหรือไม่ ?

        

 ถึงแม้ว่าทั้งความร้อนและงานจะไม่ใช่ฟังก์ชันสภาวะ แต่ผลรวมของงานและความร้อน (q + w) ซึ่งก็คือ การเปลี่ยนแปลงพลังงานภายใน (DE) ซึ่งเป็นฟังก์ชันสภาวะ ที่ไม่ขึ้นกับวิธีการเปลี่ยนแปลง แต่ขึ้นอยู่กับสภาวะสุดท้ายและสภาวะเริ่มต้นเท่านั้น

         

กฏข้อที่หนึ่งของเทอร์โมไดนามิกส์ มีพื้นฐานมาจากกฎอนุรักษ์พลังงาน ซึ่งมีใจความว่า “พลังงานสามารถเปลี่ยนจากรูปหนึ่งไปเป็นอีกรูปหนึ่งได้ แต่ไม่สามารถสร้างหรือทำให้พลังงานหายไปได้”  แล้วเราจะทราบได้อย่างไรว่า กฎอนุรักษ์พลังงานนี้เป็นจริงหรือไม่ ?         เราสามารถตรวจสอบความถูกต้องของกฎนี้ได้โดยการวัดการเปลี่ยนแปลงพลังงานภายในของระบบ (ใช้สัญลักษณ์เป็น DE หรือ DU) เทียบกับความแตกต่างระหว่างสภาวะเริ่มต้นกับสภาวะสุดท้ายของระบบ DE    =    Ef   -   Ei         ในทางเคมี เรามักจะสนใจการเปลี่ยนแปลงที่เกิดขึ้นในระบบมากกว่าในสิ่งแวดล้อม ซึ่งการเปลี่ยนแปลงพลังงานภายในของระบบ (DE) มีค่าเท่ากับผลรวมของความร้อน (q) กับงาน (w) ดังนี้ (q มีค่าเป็นบวกสำหรับกระบวนการดูดความร้อน และมีค่าเป็นลบสำหรับกระบวนการคายความร้อน)         กฏข้อที่หนึ่งของเทอร์โมไดนามิกส์  กล่าวว่า "พลังงานรวมของทั้งระบบและสิ่งแวดล้อมต้องมีค่าคงที่ แต่พลังงานสามารถเปลี่ยนรูปจากรูปหนึ่งไปเป็นอีกรูปหนึ่งได้"  นักเรียนคิดว่า การเปลี่ยนแปลงพลังงานภายในของระบบปิด ระบบเปิด และระบบโดดเดี่ยว จะมีค่าเท่ากันหรือแตกต่างกัน อย่างไร ?          ความร้อน (q) และงาน (w) เป็นตัวแปรสำคัญในการเปลี่ยนแปลงพลังงานภายในของระบบ (DE)         การเปลี่ยนแปลงพลังงานภายในของระบบปิดจะมีค่าเท่ากับพลังงาน (งานและความร้อน) ที่ผ่านเข้า-ออกรอยต่อของระบบกับสิ่งแวดล้อม         พลังงานภายในของระบบโดดเดี่ยว (isolated system) จะมีค่าคงที่  นักเรียนคิดว่า การเปลี่ยนแปลงพลังงานภายในของกระบวนการที่เกิดภายใต้สภาวะปริมาตรคงที่ และกระบวนการที่เกิดภายใต้สภาวะความดันคงที่ น่าจะเท่ากันหรือแตกต่างกัน อย่างไร ?         จากสมการ DE       =    q   +   w           กระบวนการที่เกิดภายใต้สภาวะปริมาตรคงที่ (isochoric process) หรือ DV = 0 จะไม่มีงานเกิดขึ้นในการเปลี่ยนแปลงนี้ (ความดันบรรยากาศ)         จะได้ว่า  DE    =    q   +   (- PDV)    =     qv                         (PDV    =    0) (qv หมายถึง q ที่เกิดภายใต้สภาวะปริมาตรคงที่)         นั่นคือ การเปลี่ยนแปลงพลังงาน (DE) จะเท่ากับปริมาณความร้อนที่ถ่ายเท (q)           กระบวนการที่เกิดภายใต้สภาวะความดันคงที่ (isobaric process)หรือ DP = 0 ปฏิกิริยาส่วนใหญ่เกิดขึ้นภายใต้สภาวะความดันคงที่          ถ้าปฏิกิริยานั้นทำให้จำนวนโมลของแก๊สเพิ่มมากขึ้นกว่าเริ่มต้น แก๊สก็จะขยายตัวดันสิ่งแวดล้อมออกไปในทิศทางต้านกับความดันบรรยากาศ (ระบบขยายตัว) เราถือว่าระบบทำงานให้กับสิ่งแวดล้อม          ถ้าปฏิกิริยานั้นใช้จำนวนโมลของแก๊สมากกว่าแก๊สที่เกิดจากปฏิกิริยา ความดันบรรยากาศภายนอกก็จะดันระบบเข้ามา (ระบบหดตัว) เราถือว่าสิ่งแวดล้อมทำงานให้กับระบบ          แต่ถ้าปฏิกิริยาใดที่ไม่เกี่ยวข้องกับการใช้แก๊สและไม่มีแก๊สเกิดขึ้น การเปลี่ยนแปลงปริมาตร ก็จะเกิดขึ้นน้อยมากจนอาจถือได้ว่า DV = 0 ตัวอย่างปฏิกิริยาที่เกิดภายใต้สภาวะความดันคงที่         การใส่โลหะโซเดียม ชิ้นเล็กๆ ลงในบีกเกอร์ที่มีน้ำอยู่ จะเกิดปฏิกิริยาอย่างรวดเร็ว ซึ่งสมการที่เกิดขึ้นคือ         การเปลี่ยนแปลงพลังงานในปฏิกิริยานี้ คือ DE ผลิตภัณฑ์ที่เกิดขึ้นคือ แก๊สไฮโดรเจน ซึ่งจะดันอากาศภายในกระบอกสูบออกไปและดันลูกสูบให้ลอยขึ้น ต้านกับความดันบรรยากาศภายนอก (Pext) ซึ่งปริมาตรที่เปลี่ยนแปลง คือ DV ส่วนความร้อนของปฏิกิริยาที่ความดันคงที่จะมีเท่ากับการเปลี่ยนแปลงเอนทัลปี (qp = DH)  ถ้าเราใช้โลหะโซเดียมปริมาณมากกว่าเดิม ผลการทดลองจะเป็นอย่างไร จะเป็นไปตามหลักการของกระบวนการที่สภาวะความดันคงที่หรือไม่ ? หมายเหตุ: ถ้าใช้โลหะโซเดียมขนาดใหญ่ ปฏิกิริยาจะเกิดขึ้นอย่างรุนแรงและอาจดันลูกสูบกระเด็นหลุดออกได้ ดังนั้น ในการทำการทดลองควรใช้โลหะโซเดียมขนาดเล็กๆ หรือทำปฏิกิริยากันที่ความเข้มข้นต่ำๆ หมายเหตุ :  การเปลี่ยนแปลงเอนทัลปี (DH) คือ ปริมาณความร้อนที่ผ่านเข้าหรือออกจากระบบในกระบวนการที่ความดันคงที่ ที่มา:http://www.sa.ac.th/winyoo/thermo_gas/Thermal/thermal.htm